Ashay Dharwadker,
The Four-Color Theorem,
and Usenet Postings
by Steven H. Cullinane
July 25, 2005
a pathological liar,
a sociopath,
a crank,
a nut,
someone who should be "locked up in gitmo,"
a moron,
a lunatic,
a fraudster,
paranoid,
an idiot,
stupid,
a pompous fool,
and evil.
The above may be of some use to students of crankery.
* For the trail that leads from my critique of Dharwadker to the above list of epithets, see
Non-computer proof of 4 color Theorem,
2000 Oct. 13-Nov. 30,
sci.math, 23 posts
Open Directory Abuse,
2002 Oct. 2-Oct. 14,
sci.math, 8 posts
Open Directory Abuse,
2002 Oct. 2-Oct. 15,
comp.misc, 2 posts
Steven Cullinane is a Liar,
2002 Nov. 1-Nov.16,
geometry.research, 2 posts
Four-colour proof claim,
2003 Aug. 10-Sept.1,
sci.math, 9 posts
Proof of 4 colour theorem No computer!!!,
2003 Aug. 10-Aug. 20,
alt.sci.math.combinatorics, 8 posts
Steven Cullinane is a Crank,
2005 July 5-July 21
sci.math, 70 posts
Update of August 4, 2005:
The name "Bob Stewart," apparently a pseudonym, appears in postings to the above topic "Steven Cullinane is a Crank." The "Stewart" postings there contain the epithets "lunatic," "fraudster," "paranoid," "idiot," "stupid," "pompous fool," and "crank."
A possible connection of "Bob Stewart" to Dharwadker --
Yesterday I noticed a new site,
The Four Color Theorem - A Review
The site's author is "Robert Stewart."
A related site that has existed for some time,
Update of August 5, 2005:
The new web page by "Robert Stewart" discussed above is dated July 31, 2005.
Also on July 31, "Bob," rather than "Robert," "Stewart" posted an item at the newsgroup sci.math that said he was a "working mathematician" interested in the implications of Gödel's incompleteness theorem. Here is my response to that posting.
From Math Forum's sci.math postings --
http://mathforum.org/kb/message.jspa?messageID=3874695&tstart=0#reply-tree
Re: What does Gödel's Incompleteness mean for the Working Mathematician?
Posted: Aug 3, 2005 1:33 PM
By: Steven H. Cullinane
"Bob Stewart" asked on July 31, 2005, "What does Gödel's incompleteness mean for the working mathematician?"
"Stewart" supplied as background a passage he plagiarized from Carl Boyer's "A History of Mathematics."
Here is "Stewart"'s version:
"Gödel showed that within a logical system, propositions can be formulated that are undecidable or undemonstrable within the axioms of the system. That is, within the system, there exist certain clear-cut statements that can neither be proved nor disproved. Hence one cannot, using the usual methods, be certain that the axioms will not lead to contradictions."
Here is Boyer's version:
"Gödel showed that within a rigidly logical system such as Russell and Whitehead had developed for arithmetic, propositions can be formulated that are undecidable or undemonstrable within the axioms of the system. That is, within the system there exist certain clear-cut statements that can neither be proved nor disproved. Hence, one cannot, using the usual methods, be certain that the axioms of arithmetic will not lead to contradictions." (Wiley paperback, 2nd edition, 1991, page 611)
"Hence"? This nontrivial "hence" of Boyer's conceals some history of enduring interest. It suggests the startling conclusion that
"... there is no rigorous justification for classical mathematics."
"Stewart" may, of course, dismiss this conclusion as the ravings of a crank. (See "Stewart"'s recent sci.math postings.)
For more on Boyer's "hence" and "rigorous justification," see
http://hps.elte.hu/~redei/cikkek/ems.pdf.
Further remarks by "Robert Stewart" on Dharwadker's "proof" may be found at the Wikipedia discussion of the four-color theorem.
Here is a sample of that discussion. "Stewart" is attacking mathematician Jitse Niesen, who has questioned Dharwadker's "Lemma 8" proof:
"It is a trivial exercise to show that distinct left coset representatives always belong to distinct right cosets. Are you familiar with elementary Group Theory?"
As the context shows, "Stewart" means to say that "representatives of distinct left cosets always belong to distinct right cosets." But, as Niesen points out, this is false. For an example, see the discussion of elementary properties of cosets at a web page on quotient groups titled "Lab6.htm" at the Journal of Online Mathematics. The figure below, taken from that web page, shows the cosets of a two-element subgroup K of S3. Note that r1 and m2 belong to distinct left cosets but do not belong to distinct right cosets.
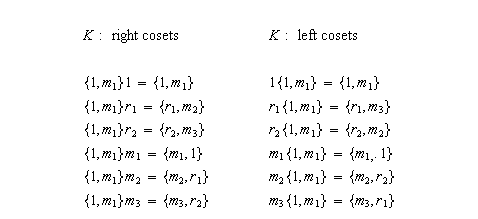
To check this table, replace
r1 by (abc),
r2 by (acb),
m1 by (ab),
m2 by (ac),
m3 by (bc).
Then we have, for the right cosets above,
m1r1=(ab)(abc)=(ac)=m2,
m1r2=(ab)(acb)=(bc)=m3,
m1m1=(ab)(ab)=1,
m1m2=(ab)(ac)=(abc)=r1,
m1m3=(ab)(bc)=(acb)=r2,
and for the left cosets above,
r1m1=(abc)(ab)=(bc)=m3,
r2m1=(acb)(ab)=(ac)=m2,
m1m1=(ab)(ab)=1,
m2m1=(ac)(ab)=(acb)=r2,
m3m1=(bc)(ab)=(abc)=r1.
"Stewart"'s further remarks to Niesen seem relevant:
"You have just shown above that you are not familiar with the elementary properties of cosets! How are you going to check Dharwadker's proof?"
Updates of September 7-11, 2005:
Remarks related to the above discussion of cosets--
Two Opposing Views
by Steven H. Cullinane,
Sept. 7, 2005
From "Common Systems of Coset Representatives,"
by Ashay Dharwadker, Sept. 2005, at
http://www.geocities.com/dharwadker/coset.html --
| "Using the axiom of choice, we prove that given any group G and subgroup H, there always exists a common system of coset representatives of the left and right cosets of H in G." |
From "Hopf Algebra Extensions and Monoidal Categories" (pdf),
by Peter Schauenburg, at
http://www.mathematik.uni-muenchen.de/~schauen/papers/haemc.pdf --

Update of Sept. 11, 2005:
Dharwadker has changed his claim. He now says,
|
"Using the axiom of choice, we prove that given any group G and a finite subgroup H, there always exists a common system of coset representatives of the left and right cosets of H in G." |
This new claim avoids the difficulty described by Schauenburg above, since H is now assumed to be finite. It also meets the following conditions stated by Fred Galvin (sci.math, Feb. 20, 2003):
|
"... if H is a finite subgroup of a (finite or infinite) group G, then there is a common transversal for the system of left cosets and the system of right cosets. This is still true for an infinite subgroup of finite index, but it breaks down for infinite subgroups of infinite index. See L. Mirsky, Transversal Theory, Academic Press, 1971, ISBN 0-12-498550-5." |